Guide de l’utilisateur Naval Designer

6. Courbure gaussienne et surfaces développables

Naval Designer donne des informations sur la courbure des surfaces grâce à un dégradé de couleurs.

1. Définition de la courbure gaussienne

En chaque point d'une surface, la courbure est mesurée dans toutes les directions.

Le produit de la courbure maximale avec la courbure minimale est appelé courbure gaussienne.

Dans le cas d'une bosse, la courbure gaussienne est positive,
dans le cas d'une selles de cheval" (hyperbole) la courbure gaussienne négative,
dans le cas d'un cylindre ou d'un cône, la courbure gaussienne est nulle partout.

2. Visualisation

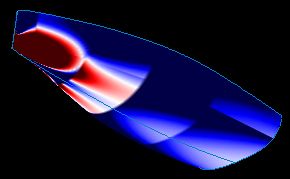
Plus la couleur est foncée, plus la courbure est importante. Si la couleur est blanche, la surface est localement développable.

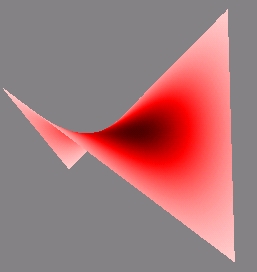
La couleur bleue met en évidence des bosses (courbure gaussienne positive) et la couleur rouge met en évidence des "selles de cheval" (courbure gaussienne négative).

Bosse en bleu
(Gaussienne positive)

Selle de cheval en rouge
(Gaussienne négative)

L'échelle des couleurs représente une plage de valeurs de courbure gaussienne (de Valeur Max à -Valeur Max). Il est possible de faire varier la sensibilité de l'affichage au niveau de courbure en faisant varier la Valeur Max. Pour cela on utilise le seuil supérieur et le curseur de réglage de la valeur Max.

Le curseur permet de faire varier en pourcentage la valeur Max de Seuil supérieur de 100% à 1% du seuil supérieur.

La valeur Max est une valeur au dessus de laquelle la valeur de la gaussienne est écrêtée. Toutes les valeurs de gaussienne au dessus prennent la couleux maximale (rouge ou bleu sombre).

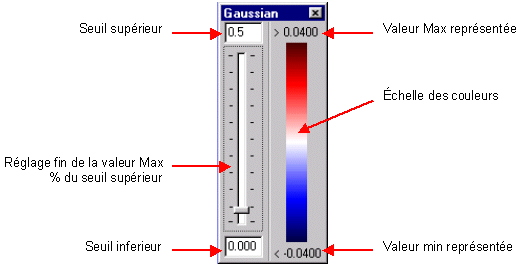
Le seuil inférieur indique un niveau de gaussienne en dessous duquel on considère que la surface est développable. Toutes les valeurs en dessous du seuil inférieur sont représentées en blanc. Cette valeur n'est pas influencée par le curseur de réglage de la valeur Max.
Dans l'image ci-dessous de la carène par défaut, le seuil est fixé à 0,05. Le dégradé de couleur est écrêté dans l'intervalle [ -0,05 ; 0,05 ].

Note : il peut être intéressant de désactiver le lissage à l'écran.

3. Définition d'une surface développable

Une surface développable est une surface que l'on peut mettre à plat sans étirement. Autrement dit, on peut représenter une surface développable par une feuille de papier, de contreplaqué ou une tôle d'acier. A l'inverse, une surface non développable ne peut être mis à plat, l'exemple le plus simple est celui de la sphère.

Une surface est réglée si et seulement si par tout point il passe au moins une droite entièrement contenue dans la surface.

Une surface développable est composée de portions de cônes et de cylindres.
Le cône est une surface réglée dont toutes les droites (appelées directrices) sont concourantes au sommet. Les directrices s'appuient sur le sommet et sur un cercle non coplanaire avec le sommet.
Le cylindre est une surface réglée dont toutes les directrices sont parallèles à l'axe.

Une surface développable est composée de droites dites génératrices ou directrices. Ces droites appartiennent à la surface et soit elles sont parallèles les unes avec les autres (elles forment un cylindre), soit elles se rejoignent en un point (elles forment un cône). Sur une surface NURBS développable, les droites qui forment les mailles (les isoparamétriques) "dans le sens de l'ordre 2" sont des génératrices.

4. Application aux surfaces développables

Voici l'exemple du célèbre Muscadet, voilier à deux bouchains.

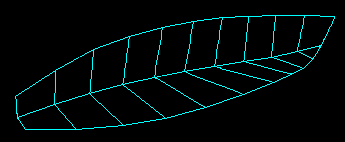
Dans le cas d'une surface développable (composée de portions de cylindre et de cônes) la courbure gaussienne est nulle. Elle est représentée dans Naval Designer par la couleur blanche.

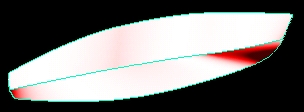
On remarque que le bouchain supérieur est parfaitement développable. Le bouchain inférieur n'est pas développable au niveau du tableau arrière et surtout au niveau de l'étrave.
Ce bateau est néanmoins construit à des milliers d'exemplaire... comment est-ce possible ?
Les matériaux ont tous une souplesse relative, ce qui permet de les ployer dans les deux sens, dans un sens de manière importante, et faiblement dans l'autre.
Ainsi on peut admettre "une certaine non développabilité" localement sur une surface. Mais le seuil admissible dépend du matériau. Aucune règle n'étant disponible, l'expérience prévaut.

Le rôle de l'architecte est de minimiser au maximum la courbure gaussienne de manière à ce que le constructeur ne soit pas obligé à faire des acrobaties, voire à tricher un peu.

Une petite maquette en papier cartonné est parfois utile pour valider la faisabilité de la construction.

5. Application aux surfaces non développables

Les surfaces peuvent présenter un aspect lissé et avoir des inversions de courbures invisibles dans le Studio. L'analyse par visualisation de la courbure gaussienne permet de détecter ces variations de courbure.

Ces variations peuvent être dues à la position des vertex, à leur poids, ou encore aux ordres transverses et longitudinaux de la NURBS.

Exemple d'une surface d'ordre 3x3 : l'ordre faible et le nombre élevé de colonnes de vertex provoque des discontinuités de courbure au sein de la NURBS. L'augmentation de l'ordre transversal et longitudinal permettra la correction du défaut.

Rappel sur les NURBS :

L'ordre 2 implique une discontinuité.
L'ordre 3 implique une continuité de la courbe, mais pas celle de la dérivée 1.
L'ordre 4 implique une continuité de la courbe et celle de la dérivée 1, mais pas celle de la dérivée 2.
L'ordre 5 implique une continuité de la courbe et celle des dérivée 1 et 2, mais pas celle de la dérivée 3.

Le calcul de la courbure gaussienne nécessite le calcul des dérivées secondes, donc il faut un ordre 5 pour s'assurer d'avoir dans tous les cas une gaussienne "douce". Mais avoir une gaussienne "douce" n'est pas une condition obligatoire !

Dans l'exemple précédent on a remplacé l'ordre 3x3 par 5 (longitudinal) x 4 (transversal) :

La courbure est alors continue.

Attention, la forme de la carène a changé en même temps que le changement d'ordre. Il est préférable de prévoir dès le départ un ordre suffisamment élevé si l'on sait que le nombre de lignes ou de colonnes de vertex sera important.

D'autre part, le contrôle d'une surface d'ordre plus élevé est un peu plus délicat.

Rappel : il est préférable d'avoir un filet de vertex régulier, cela permet d'éviter des déformations peu visibles à l'écran.

7. Développement de surfaces développables

Une fois l'assurance acquise qu'une surface est développable grâce à sa courbure gaussienne nulle en tout point, il est intéressant de développer cette surface, c'est-à-dire la mettre à plat, pour envisager la construction. Il s'agit donc de l'aboutissement du processus de conception d'une coque à bouchains vifs.

Choisir le menu Surfaces/Développement... la liste des surfaces potentiellement développables apparaît.

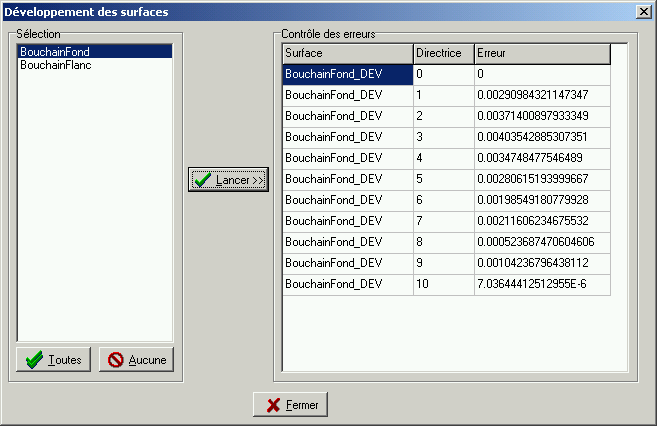
Cette liste contient toutes les surfaces dont la flexibilité (l'ordre) transversale ou longitudinale vaut 2 et dont le nombre de lignes et respectivement de colonnes est égalemement égal à deux.
Si le nombre de lignes est supérieur à deux (plus d'un bouchain), il faut dupliquer la surface autant de fois qu'il y a de bouchains et pour chaque surface obtenue supprimer les lignes excédentaires de manière à ce que chaque bouchain soit représenté par une surface à deux lignes de vertex.

Attention, la présence des surfaces dans la liste ne garantie pas que la surface est réellement développable.

En cliquant sur le bouton "Lancer>>", les surfaces sélectionnées dans la liste sont développées.
Ce processus crée de nouvelles surfaces et le tableau des erreurs de développement est rempli.
Le tableau contient une ligne par génératrice développée. Le nombre de génératrices est directement lié à la précision utilisée pour l'affichage.

Dans une surface développable, les isoparamétriques (lignes du maillage) sont les directrices, et les extrémités de deux directrices adjacentes (4 points) sont contenus dans le même plan. Pour une surface qui ne seraît pas parfaitement développable, ces 4 points peuvent ne pas appartenir au même plan. En développant on ramène les 4 points dans le même plan, ce qui provoque une distorsion. On évalue la distorsion en faisant la différence de longueur des génératrice avant et après développement. C'est cette distorsion qui est affichée dans ND dans la colonne "Erreur".
Dans l'exemple ci-dessus, l'erreur maximale est de 4mm environ, mais l'erreur se cumule de génératrice en génératrice.

On obtient ceci :

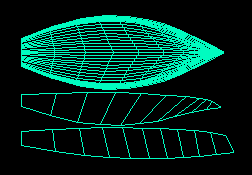
<< Précédent | Début | Suite >